Todo mês, quando saem os dados de homicídios em São Paulo apontando o crescimento das mortes, acontece a mesma dança. Quase um Gangnam Style estatístico.
Passo 1: a Secretaria da Segurança convoca uma coletiva
Passo 2: a imprensa compara com um período anterior e faz a crítica.
Passo 3: as autoridades dizem que a comparação com o mês anterior não é a correta, que a correta é a comparação com o ano anterior (se for menos desfavorável). Se a comparação desfavorável for com o ano, eles sugerem comparar com o mês, pra ficar bem na foto.
Passo 4: o problema continua. O discurso oficial vitorioso também. Mês que vem toca de novo a nossa música.
Neste mês, o secretário da Segurança Pública, Antônio Ferreira Pinto, se queixou:
“Se você comparar com o mês passado, houve um aumento de 3%. Mas, se pega um número maior, que dá mais repercussão, como do ano passado pra cá, aí aumentou significativamente.”
O que é mais certo, comparar com o mês ou com o ano?
Os repórteres da Folha foram olhar o manual de interpretação da própria Secretaria de Segurança:
No documento “Estatística da Criminalidade – Manual de Interpretação”, elaborado pela Coordenadoria de Análise e Planejamento, a “recomendação é que comparem, sempre que possível, períodos equivalentes de tempo” –ou seja, setembro com setembro e não setembro com agosto.
Discordo em parte da interpretação dos meus colegas. “Períodos equivalentes de tempo” é ambíguo o bastante para legitimar tanto a comparação com o mês quanto a comparação com o ano. As duas são legítimas, embora contem histórias diferentes – ou pedaços diferentes da mesma história.
Eu gosto de olhar a história mais completa possível. Por isso, prefiro olhar a série histórica mais longa que tiver em mãos, para ver a evolução inteira da série registrada. É a diferença entre olhar o filme inteiro e comparar dois fotogramas.
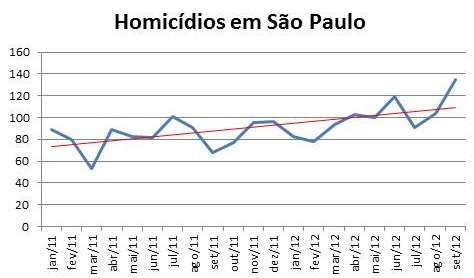
Veja este gráfico que eu fiz a partir do nosso excelente Radar da Violência:
Observando a linha azul, você vê que há meses de queda, e nesses meses de queda as autoridades comemoram. Esses meses de queda são seguidos por meses de aumento. Nesses, as autoridades dizem haver má-vontade da imprensa.
Observando a linha vermelha, você vê a tendência da curva. E a tendência é de aumento.
Em média, nessa série histórica, há 91 homicídios por mês. Com 135, setembro esteve bem acima da média.
O desvio-padrão, medida que dá uma “média” do quanto cada mês se distancia da média, é de 17,2 homicídios para mais ou para menos. Pense nisso mais ou menos como na margem de erro das pesquisas de opinião.
Se a evolução dos homicídios por mês em São Paulo seguir a distribuição normal – digamos que siga -, a maioria dos meses (68%, se a regra for seguida à risca, mas a série é pequena) deve ter entre quase 74 e pouco mais de 108 homicídios.
Nos 21 meses da amostra, 17 tiveram entre 74 e 108 homicídios. Dois ficaram abaixo dessa faixa (ambos em 2011). Dois ficaram acima dessa faixa (ambos em 2012).
O dado de setembro é bastante alto, mas não é um “ponto fora da curva”, expressão que o chefe da Polícia Civil usou para justificar a queda dos homicídios em março de 2011. Ponto fora da curva é quando o dado está mais de três desvios-padrão acima ou abaixo da média. Ou seja: mais de 142,7 e menos de 39,2 homicídios.
Usar o termo “ponto fora da curva” nesse contexto é abusar da sofrida matemática dos jornalistas pra dar uma aspa sonora que não explica nada, sabendo que ela será publicada de qualquer jeito. Os 135 homicídios deste mês são um ponto dentro da curva – apesar de bastante alto -, assim como o foram os 53 de março de 2011.
Digo até mais.
Conhecendo o conceito de regressão à média, posso pedir licença à Barbara Gancia e apostar um picolé de limão com você.
Aposto que em breve haverá uma redução. Essa redução levará os homicídios para perto dos 91, e o governo vai comemorar. Aí depois vai aumentar de novo, talvez para além dos 135 atuais, e o governo vai dizer que a imprensa está de má vontade. E o Gangnam Style estatístico vai tocar de novo, todo mês.
Claro que não tenho uma bola de cristal. Apenas entendo a lógica da regressão à média.
Quer conhecer melhor o conceito? A revista Cálculo publicou recentemente um bom texto a respeito.